Задачи уровня Малыш-3,4 классы, III уровень сложности

Задача 17

Четыре подружки сидят на лавочке. Сначала Маша поменялась местами с Дашей. Потом Даша поменялась местами с Ирой. Если называть девочек слева направо, то подруги расположились в таком порядке: Маша, Соня, Даша и Ира. В каком порядке слева направо девочки сидели на лавочке сначала?

Варианты ответа:

А: Маша, Соня, Ира, Даша 

Б: Ира, Соня, Маша, Даша 

В: Даша, Соня, Маша, Ира 

Г: Соня, Даша, Ира, Маша

Д: Даша, Соня, Ира, Маша

Задача 18

Олег, Володя, Дмитрий, Андрей, Роман и Тарас по одному разу бросают кости. У каждого из них выпадает разное количество точек. У Олега вдвое больше точек, чем у Володи, и втрое больше, чем у Дмитрия. У Андрея выпало в четыре раза больше точек, чем у Романа. Сколько точек выпало у Тараса?

Варианты ответа:

А: 2 Б:3 В: 4 Г: 5 Д: 6

Задача 19

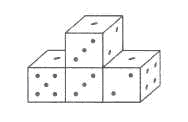Сумма количеств точек, расположенных на противоположных гранях кубика, равняется 7. Из четырех одинаковых игральных кубиков образовали фигуру так, как показано на рисунке. Как будет выглядеть эта фигура, если посмотреть на нее с противоположной стороны?

Варианты ответа:

Задача 20

Даны три карточки, изображенные на рисунке. Из них можно создавать разные числа, например 989 или 866. Сколько разных трёхзначных чисел можно образовать, используя эти карточки?

Варианты ответа:

А: 4 Б: 6 В: 8 Г: 9 Д: 12

Задача 21

Садовник посадил 8 деревьев в ряд на расстоянии 5 метров друг от друга. Рядом с первым деревом есть колодец. Для поливки двух деревьев нужно одно ведро воды. Какой наименьший путь надо преодолеть садовнику, чтобы полить все деревья, пользуясь одним ведром?

Варианты ответа:

А: 40 Б: 80 В: 105 Г: 125 Д: 155

Задача 22

В коробке лежат карандаши - 7 красных и 5 синих. Какую наименьшее количество карандашей надо взять наугад, чтобы среди них было не менее двух красных и не менее трех синих?

Варианты ответа:

А: 5 Б: 7 В: 9 Г: 10 Д: 12

Задача 23

Дима написал числа 6, 7 и 8 в кругах, как показано на рисунке. Он хочет еще дописать числа 1, 2, 3, 4 и 5 в других кругах так, чтобы сумма чисел на каждой стороне квадрата была равна 13. Чему равна сумма чисел, расположенных в серых кругах?

Варианты ответа:

А: 12 Б: 13 В: 14 Г: 15 Д: 16

Задача 24

Каждая часть прямоугольника, изображенного на рисунке рядом, закрашена одним из четырех цветов: красным (К), синим (С), зеленым (3) или желтым. Каждые две части, имеющие общую границу, закрашены разными цветами. Для некоторых частей указан их цвет. Какого цвета часть, обозначенная буквой X?

Варианты ответа:

А: красного Б: синего В: зеленого Г: желтого Д: невозможно определить

Задачи уровня Малыш-3,4 классы, II уровень сложности

Задача 9

Лист бумаги согнули пополам по черной линии. Какая буква не попадет на чёрный квадратик? 

Варианты ответа:

А: А Б: Б В: В Г: Г Д:Д

Задача 10

Во время вечеринки два одинаковых торта разрезали на четыре равные части каждый. Затем каждую часть еще разделили на три равные части. Каждый из присутствующих получил по куску торта, и три куска остались. Сколько человек было на вечеринке?

Варианты ответа:

А: 13 Б; 18 В: 21 Г: 24 Д: 27

Задача 11

Длина дорожки АD - 15 м. На ней обозначены точки В и С. АС = 7 м, ВD = 10 м. Вычислите длину ВС.

Варианты ответа:

А: 1 м Б: 2 м В: 3 м Г: 4 м Д: 5 м

Задача 12

У хозяйки есть лотки, рассчитанные на 5 яиц и на 10 яиц. Какое наименьшее количество лотков надо взять хозяйке, чтобы разложить 55 яиц?

Варианты ответа:

А: 5 Б: 6 В: 9 Г: 11 Д: 13

Задача 13

Все четырехзначные числа, которые записываются с помощью двух единиц, одного нуля и одной двойки, выписали в ряд в порядке возрастания. На каком месте в этом ряду будет стоять число 2011?

Варианты ответа:

А: 4 Б: 5 В:6 Г:7 Д: 8

Задача 14

По результатам первой викторины Петр Михайлович набрал 10 баллов. Во второй викторине за правильный ответ на каждый из 10 вопросов начисляют 1 балл, а за каждый неправильный - снимают 1 балл. Сколько неправильных ответов дал Петр Михайлович во второй викторине, за обе викторины он набрал 14 баллов?

Варианты ответа:

А:3 Б:4 В:5 Г:6 Д:7

Задача 15

Андрюша записывает буквы слова KANGAROO в ячейках таблицы. В каждой клетке только одну букву. Первую букву он пишет где угодно. Каждую следующую букву - в ячейке, имеющей общую сторону или общую вершину с предыдущей ячейкой. Какую из предложенных таблиц не может получить Андрюша?

Варианты ответа:

Задача 16

У каждого ученика класса дома одно или два животных. У всех вместе у них восемь котят, шесть собачек и три рыбки. У двух учеников дома есть по собачке и рыбке, у трех - по котенку и собачке. У всех остальных по одному животному. Сколько учеников в классе?

Варианты ответа:

А: 11 Б: 12 В: 13 Г: 14 Д: 17

Задачи уровня Малыш-3,4 классы, I уровень сложности

Задача 1

Боря пишет слово КЕНГУРУ: по одной букве каждый день. Он начал писать в среду. В какой день недели он закончит писать все слово? 

Варианты ответа:

А: в понедельник Б: во вторник В: в среду Г: в четверг Д: в пятницу

Задача 2

Сколько килограммов нужно прибавить на правую чашу весов, изображенных на рисунке, чтобы установить их в положение равновесия?

Варианты ответа:

Задача 3

Кенгуру прыгает по клеткам. Вначале он прыгнул на одну клетку вправо, потом на одну вверх, далее на одну влево, а затем на одну вниз и еще раз на одну вправо. Где оказался Кенгуру в конце движения?

Варианты ответа:

Задача 4

Ваня проснулся полтора часа назад. Через три с половиной часа отправляется поезд, которым мальчик едет к бабушке. За сколько времени до отправления поезда проснулся Ваня?

Варианты ответа:

А: за два часа Б: за три с половиной часа В: за четыре часа Г: за четыре с половиной часа Д: за пять часов

Задача 5

На листе бумаги в клеточку Петя нарисовал пять фигурок (см. ответы). Какая из фигурок содержит в себе наибольшее число клеток, если две половинки клетки равны одной клетке?

Варианты ответа:

Задача 6

Аленка заплатила 12 гривен и 60 копеек за три порции мороженого «Пломбир». Миша заплатил 4 гривны и 60 копеек за два стакана сока «Ягодка». Сколько Игорь заплатил за одну порцию мороженого «Пломбир» и один стакан сока «Ягодка»?

Варианты ответа:

А: 4 грн. 00 коп. Б: 4 грн. 20 коп. В: 5 грн. 00 коп. Г: 5 грн. 50 коп. Д: 6 грн. 50 коп.

Задача 7

Когда наступает целый час (1:00, 2:00, 3:00 и т.д.), часы отбивают соответствующее количество ударов (1 раз, 2 раза, 3 раза и т.д.). Они также отбивают один раз в середине между целыми часами (8:30, 9:30, 10:30). Сколько ударов сделают часы от 7:55 до 10:45 того же дня?

Варианты ответа:

А: 6 Б: 18 В: 27 Г: 30 Д: 33

Задача 8

Маша выбрала одну из пяти фигур изображенных в ответах. Это не квадрат. Это или круг, или треугольник. Эта фигура тёмная. Какую из фигур выбрала Маша?

Варианты ответа:

Задания олимпиады для 2 класса на украинском языке

По просьбе читателя выкладываю сканы условий задач олимпиады Кенгуру уровня Малыш (2й класс).

Информационный вестник олимпиады Кенгуру

Региональный координаторам разосланы информационные вестники олимпиады Кенгуру-2011. В них напечатаны условия, решения и ответы всех задач олимпиады, фотографии, которые участники присылали в оргкомитет, а также список школ, где конкурс проводился наиболее массово.

Этот сборник получит каждый участник олимпиады, вне зависимости от цвета диплома.

Решение задачи К25 олимпиады Кенгуру 2011

Уровень: Кадет (7 и 8 класс)

Условие. Сколько натуральных чисел можно образовать из цифр 1, 2, 3, 4, 5, используя каждую цифру один раз, таких, что первая цифра числа делится на 1, число, образованное первыми двумя цифрами, делится на 2, первыми тремя - на 3, четырьмя - на 4, пятью - на 5?

Варианты ответа: А:0, Б:1, В:2, Г:5, Д:10,

Решение
Последняя цифра числа - обязательно пятёрка. Сумма остальных четырёх цифр числа равна 10. Т.к. сумма первых трёх его цифр должна делиться на 3, то на четвёртом месте должна стоять или 1 или 4. Единица там стоять не может, т.к. число, образованное первыми четырьмя цифрами, должно делиться на 4. Таким образом, число будет иметь вид ???45.

Поскольку число, образованное первыми двумя цифрами, должно делиться на 2, то двойка стоит на втором месте: ?2?45. Однако, что бы мы ни поставили на третье место, число из первых четырёх цифр на 4 не разделится. Значит, таких чисел не существует.

Ответ: А:0.

Летний математический лагерь

Команда Кировоградской области отправляется в летний математический лагерь "Кенгуру" в Ливадии.
На фото: Сушко Максим (г.Светловодск), Пидручна Светлана Николаевна (руководитель группы, г.Малая Виска), Сотниченко Максим (пгт. Хащувате Гайворонского района), Сербина Надежда Алексеевна (областной координатор олимпиады "Кенгуру").